Genetic Operators In Machine learning

Introduction
Overview of Evolutionary Thinking in Machine Learning
Evolutionary thinking in machine learning is inspired by the principles of natural evolution—such as survival of the fittest, adaptation, and gradual improvement over time. Instead of relying only on mathematical formulas or gradients, evolutionary approaches explore solutions by simulating how populations evolve across generations.
In machine learning, this idea is implemented through genetic algorithms and other evolutionary algorithms, where multiple candidate solutions are evaluated, improved, and refined iteratively. This approach is especially useful when problems are complex, nonlinear, or difficult to solve using traditional optimization methods.
Why Optimization Is Critical in Modern ML Systems
Optimization lies at the heart of every machine learning system. Whether it is minimizing error, maximizing accuracy, or finding the best parameters, ML models constantly search for optimal solutions. Modern ML problems often involve:
- Huge search spaces
- High-dimensional data
- Non-convex objective functions
Traditional optimization techniques may struggle in such environments. Poor optimization can lead to slow training, suboptimal performance, or models that fail to generalize well. This is why advanced optimization strategies—like evolutionary methods—play a vital role in modern machine learning workflows.
How Genetic Operators Help Machines “Learn” Better Solutions
Genetic operators such as selection, crossover, and mutation are the driving forces behind evolutionary optimization. They guide how solutions evolve over time:
- Selection chooses the best-performing solutions, ensuring quality improvement
- Crossover combines good traits from multiple solutions to create stronger offspring
- Mutation introduces randomness, helping the system explore new possibilities
Together, these operators allow machine learning systems to balance exploration and exploitation, avoid local optima, and gradually improve solution quality. Instead of learning through gradients alone, machines “learn” by evolving better solutions generation after generation—making genetic operators a powerful tool for optimization in complex ML problems.
Basics of Genetic Algorithms

What is a Genetic Algorithm?
A Genetic Algorithm (GA) is an optimization technique inspired by the process of biological evolution. Just as living organisms evolve over generations to adapt better to their environment, genetic algorithms evolve solutions to problems by gradually improving them over time.
In a genetic algorithm, each possible solution is treated as an individual in a population. These individuals compete based on how well they solve the given problem. The best-performing solutions are selected and combined to produce new solutions, leading to continuous improvement across generations.
Key components of a genetic algorithm include:
- Population: A collection of candidate solutions
- Chromosome: A structured way to represent a solution, usually stored as a string or an array of values.
- Fitness measures how well a solution performs.
- Generation: One complete cycle of evaluation and evolution
Together, these elements allow genetic algorithms to explore large and complex solution spaces efficiently.
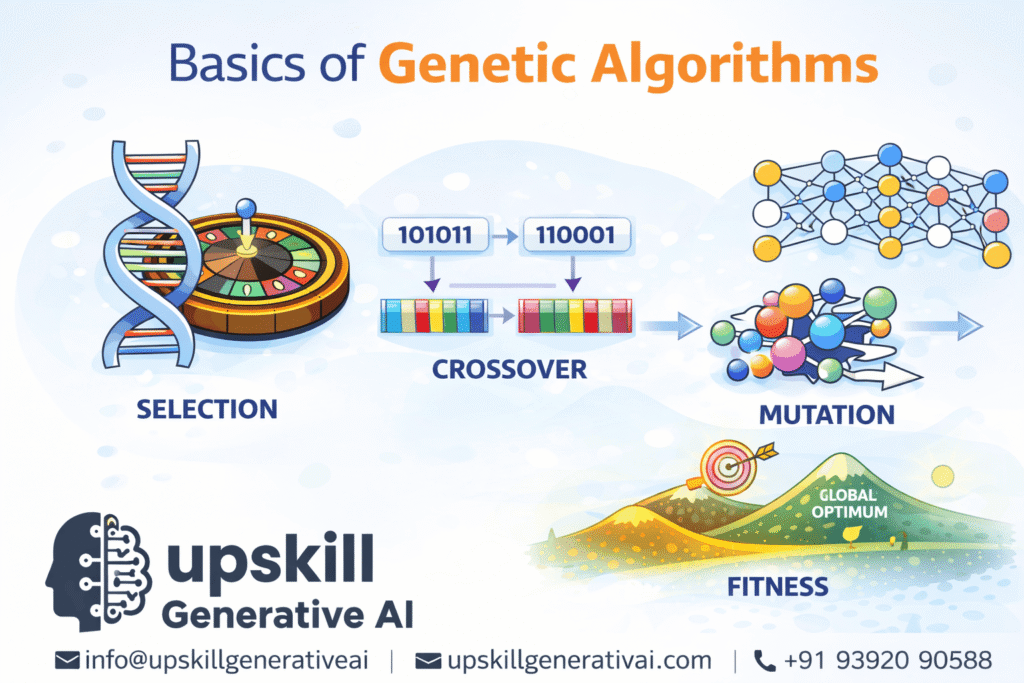
How Does a Genetic Algorithm Work? (Step-by-Step)
A genetic algorithm follows a structured evolutionary process:
Initialization
The algorithm starts by generating an initial set of randomly created candidate solutions.
This randomness ensures diversity and allows the algorithm to explore a wide range of possibilities.
Fitness Evaluation
Each solution is evaluated using a fitness function, which measures how well it performs for the given task.
Selection
The solutions with the highest fitness scores are chosen for further processing.Higher-quality solutions are more likely to be selected for reproduction.
Crossover
Selected solutions are paired and combined to create new offspring. This step allows useful traits from different solutions to be mixed together.
Mutation
Small random changes are applied to some solutions. Mutation introduces diversity and helps prevent the algorithm from getting stuck in poor solutions.
Termination
The algorithm stops when a predefined condition is met—such as reaching a maximum number of generations or achieving an acceptable fitness level.
Where Are Genetic Algorithms Used in Machine Learning?
Genetic algorithms are widely used in machine learning, especially when traditional optimization methods are ineffective.
- Optimization Problems: Solving complex, non-linear, or multi-objective optimization tasks
- Feature Selection: Identifying the most relevant features to improve model performance
- Hyperparameter Tuning: Automatically finding optimal parameter values for ML models
Because genetic algorithms do not rely on gradients and can handle noisy or incomplete data, they are highly effective for challenging machine learning problems where conventional techniques fall short.
What Are Genetic Operators?
Definition of Genetic Operators
Genetic operators are the fundamental mechanisms used in genetic algorithms to modify and evolve a population of solutions over time. They control how new solutions are created from existing ones by mimicking biological processes such as reproduction, inheritance, and mutation.
In simple terms, genetic operators determine how solutions change, improve, and adapt from one generation to the next. The most commonly used genetic operators are selection, crossover, and mutation.
Purpose Within Evolutionary Algorithms
The main purpose of genetic operators in evolutionary algorithms is to guide the search for optimal solutions. Instead of randomly trying all possibilities, genetic operators apply structured rules that:
- Promote high-quality solutions
- Maintain diversity within the population
- Encourage exploration of new solution spaces
By repeatedly applying these operators, evolutionary algorithms gradually move toward better and more efficient solutions without needing explicit problem-solving rules.
Role in Creating New Generations
Genetic operators are responsible for generating each new generation in a genetic algorithm. The process typically follows this sequence:
- Selection chooses the best-performing individuals from the current population
- Crossover combines traits from selected individuals to form new offspring
- Mutation makes small, random changes to solutions to preserve diversity and prevent the algorithm from becoming stuck in a single pattern.
This cycle ensures that each new generation is generally better adapted than the previous one, while still exploring new possibilities.
Why Genetic Operators Are the Core of GA Performance
The performance of a genetic algorithm heavily depends on how effectively genetic operators are designed and applied. Poorly chosen operators can lead to slow convergence, loss of diversity, or suboptimal results. On the other hand, well-balanced operators can:
- Speed up convergence toward optimal solutions
- Prevent premature convergence to poor solutions
- Improve solution quality and robustness
Because genetic operators directly influence learning efficiency, exploration, and optimization, they are considered the core driving force behind the success of genetic algorithms in machine learning.
Importance of Genetic Operators in Optimization
Genetic operators play a crucial role in solving optimization problems where traditional methods often struggle. By simulating evolutionary processes, these operators allow machine learning systems to search complex solution spaces efficiently and adaptively.
Inspiration from Natural Selection
Mimicking Biological Evolution
Genetic operators are directly inspired by biological evolution, where organisms evolve through reproduction, variation, and selection. In genetic algorithms, solutions evolve in a similar way. Each candidate solution represents an individual, and genetic operators guide how these individuals change over time, enabling the algorithm to improve solutions naturally rather than relying on strict mathematical rules.
Survival of the Fittest
The principle of “survival of the fittest” ensures that only the best-performing solutions influence future generations. Through selection, individuals with higher fitness scores are more likely to be chosen for reproduction. This increases the probability that strong characteristics are passed on, gradually improving the overall quality of solutions.
Adaptation Over Generations
As genetic operators are applied repeatedly, populations adapt to the problem environment. Poor solutions are gradually eliminated, while better ones are refined and combined. This iterative process enables continuous learning and adaptation, making genetic algorithms effective for dynamic and evolving optimization problems.
Why Genetic Operators Matter
Exploration vs. Exploitation
A major challenge in optimization is balancing exploration (searching new areas of the solution space) and exploitation (refining known good solutions). Genetic operators achieve this balance naturally:
- Crossover exploits existing high-quality solutions
- Mutation encourages exploration by introducing randomness
This balance ensures steady progress without losing innovation.
Avoiding Local Optima
Many optimization problems contain multiple local optima. Traditional optimization techniques may get stuck in these suboptimal solutions. Genetic operators, especially mutation and population diversity, help the algorithm escape local optima and continue searching for better global solutions.
Continuous Improvement
Genetic operators enable gradual and consistent improvement across generations. Even small enhancements accumulate over time, leading to significantly better solutions. This makes genetic algorithms highly effective for complex machine learning optimization tasks where incremental learning is essential.


Click Here : MLOPS Training in Hyderabad
Types of Genetic Operators
Genetic operators define how solutions evolve within a genetic algorithm. Each operator plays a distinct role in balancing solution quality, diversity, and convergence speed. Together, they form the foundation of evolutionary optimization in machine learning.
Selection Operator
Purpose of Selection
The selection operator plays a crucial role in genetic algorithms by identifying and choosing the most fit individuals from the existing population to participate in the creation of the next generation.
These selected individuals act as parents for the next generation. The main goal of selection is to ensure that high-quality solutions have a greater chance of passing their characteristics to future generations.
Common Selection Techniques
- Roulette Wheel Selection
Individuals are selected based on probability proportional to their fitness. Better solutions have a higher chance of being chosen, but weaker solutions still have a small opportunity, maintaining diversity. - Tournament Selection
A small set of individuals is randomly selected, and the top-performing individual from this group is chosen. - This method is simple, efficient, and provides good control over selection pressure.
- Rank-Based Selection
Individuals are ranked according to fitness, and selection probability is assigned based on rank rather than raw fitness values. This prevents domination by extremely fit individuals.
Impact on the Next Generation
Selection strongly influences how fast the algorithm converges. Aggressive selection can speed up convergence but may reduce diversity, while balanced selection helps maintain a healthy trade-off between convergence speed and population diversity.
Crossover (Recombination) Operator
Purpose of Crossover
Crossover is a genetic operation that merges selected traits from two parent solutions to produce new offspring solutions. The objective is to merge good traits from different solutions, potentially producing offspring that perform better than their parents.
Types of Crossover Techniques
- Single-Point Crossover
A single crossover point is chosen, and genetic material is exchanged between parents. - Multi-Point Crossover
Multiple crossover points are used, allowing more complex mixing of genetic information. - Uniform Crossover
Each gene is selected from either parent with equal probability, promoting higher diversity.
Importance of Crossover
Crossover preserves useful genetic information while enabling new combinations of traits. This process significantly improves the algorithm’s ability to explore promising regions of the solution space and generate better offspring.
Mutation Operator
Definition and Purpose
Mutation introduces small random changes to individual solutions. Unlike crossover, which recombines existing information, mutation creates entirely new variations, ensuring continued exploration.
Maintaining Genetic Diversity
Mutation prevents the population from becoming too similar. Without mutation, genetic algorithms risk stagnation and loss of innovation.
Types of Mutation Techniques
- Bit-Flip Mutation
Commonly used for binary representations, where bits are flipped randomly. - Swap Mutation
Two genes exchange positions, often used in sequencing problems. - Gaussian Mutation
Small random values from a Gaussian distribution are added, suitable for continuous parameters.
Avoiding Local Minima
Mutation helps genetic algorithms escape local optima by introducing new traits that may lead to better global solutions, keeping the optimization process active and adaptive.
Elitism Operator
Purpose of Elitism
Elitism ensures that the best-performing individuals are directly carried over to the next generation without modification. This guarantees that high-quality solutions are not lost during evolution.
Advantages and Disadvantages
- Advantages: Faster convergence and guaranteed solution quality preservation.
- Disadvantages: Excessive elitism may reduce population diversity and lead to premature convergence.
Combining Genetic Operators
Effective genetic algorithms carefully balance all operators rather than relying heavily on one.
Operator Balance Strategies
- Adjusting selection pressure
- Tuning crossover and mutation rates
Adaptive Operator Probabilities
Modern genetic algorithms dynamically adjust operator probabilities based on performance. This adaptability improves convergence speed, maintains diversity, and enhances overall optimization efficiency.
Role of Genetic Operators in Machine Learning Models

Genetic operators play a vital role in enhancing the learning and optimization capabilities of machine learning models, especially in scenarios where traditional optimization techniques are ineffective or impractical.
Why Machine Learning Models Need Genetic Operators
Non-Differentiable Optimization
Many machine learning problems involve objective functions that are non-differentiable, discontinuous, or noisy. Gradient-based methods struggle or completely fail in such cases. Genetic operators offer a gradient-free optimization approach, making them suitable for:
- Rule-based systems
- Discrete parameter spaces
- Black-box models
By evolving solutions through selection, crossover, and mutation, genetic algorithms can optimize models without relying on derivatives.
Complex Search Spaces
Modern ML models often operate in extremely large and complex search spaces with multiple local optima. Genetic operators allow simultaneous exploration of multiple regions of the solution space using a population-based approach. This parallel exploration increases the chances of discovering high-quality solutions that traditional methods might miss.
How Genetic Operators Improve Learning
Better Parameter Selection
Genetic operators enable efficient tuning of model parameters by evolving candidate parameter sets over generations. Poor-performing configurations are discarded, while promising ones are refined and combined. This results in optimized parameters that improve model accuracy and stability.
Robust Optimization
Because genetic operators rely on population diversity and randomness, they are naturally robust to noise and uncertainty. This makes genetic algorithms effective in real-world machine learning tasks where data may be incomplete, noisy, or constantly changing.
Balancing Exploration and Exploitation
One of the key strengths of genetic operators is their ability to balance exploration and exploitation during learning.
Operator Tuning Strategies
- Crossover-focused tuning improves exploitation by refining good solutions
- Mutation-focused tuning enhances exploration by introducing new variations
- Adaptive operator rates dynamically adjust probabilities based on learning progress
By carefully tuning these operators, machine learning models can learn efficiently, avoid premature convergence, and continuously improve performance across generations.
Application of Genetic Operators in Machine Learning
Genetic operators enable machine learning models to solve complex optimization tasks by evolving solutions rather than relying solely on gradient-based learning. Their flexibility makes them valuable across a wide range of ML applications.
How Genetic Algorithms Optimize ML Models
Feature Selection
In many machine learning problems, not all features contribute equally to model performance. Genetic algorithms use genetic operators to search for optimal feature subsets.
- Selection promotes feature combinations that improve accuracy
- Crossover mixes effective feature subsets
- Mutation explores new feature combinations
This process reduces dimensionality, improves generalization, and lowers computational cost.
Model Structure Optimization
Genetic operators are also used to optimize the structure of machine learning models. This includes selecting the number of layers, nodes, or connections in models such as neural networks and decision trees. By evolving architectures over generations, genetic algorithms can automatically discover model structures that deliver better performance.
Common ML Tasks Using Genetic Operators
Hyperparameter Optimization
Choosing optimal hyperparameters is a challenging task due to large and complex search spaces. Genetic operators efficiently explore these spaces by evolving hyperparameter configurations, often outperforming manual tuning and grid search methods.
Neural Network Weight Tuning
In scenarios where gradient descent is ineffective or unstable, genetic algorithms can evolve neural network weights directly. This approach, often referred to as neuroevolution, is particularly useful for reinforcement learning and dynamic environments.
Clustering and Rule Discovery
Genetic operators are applied to clustering and rule-based learning to discover meaningful groupings and interpretable decision rules. Mutation and crossover help explore diverse cluster structures and rule sets, leading to flexible and adaptive learning systems.
Real-World Examples
Financial Forecasting
Genetic algorithms are used to optimize trading strategies, forecast market trends, and select financial indicators. Their ability to adapt to changing data patterns makes them well-suited for volatile financial environments.
Scheduling Problems
In industries such as manufacturing and logistics, genetic operators help optimize complex scheduling tasks. They efficiently search for schedules that minimize time, cost, or resource usage under multiple constraints.
Bioinformatics
Genetic algorithms play a significant role in bioinformatics applications such as gene selection, protein structure prediction, and sequence alignment. Their evolutionary nature aligns well with biological data analysis.
Impact of Genetic Operators
Genetic operators have a direct and significant influence on how effectively a genetic algorithm performs in machine learning tasks. Their design and tuning determine how fast a model learns, how good the final solution is, and how well the algorithm avoids common optimization pitfalls.
Effect on Convergence Speed
Genetic operators strongly affect how quickly a genetic algorithm converges toward an optimal or near-optimal solution.
Selection pressure determines how aggressively high-quality solutions dominate future generations. Strong selection speeds up convergence but may reduce diversity.
Crossover rate influences how efficiently good traits are combined and refined.
Mutation rate can either slow convergence if too high or cause stagnation if too low.
Well-balanced operators ensure steady and efficient convergence without sacrificing exploration.
Effect on Solution Quality
The quality of the final solution depends on how effectively genetic operators explore and refine the search space.
Effective crossover preserves useful genetic information.
Controlled mutation introduces beneficial variations.
Elitism guarantees that the best solutions are not lost.
Together, these operators help genetic algorithms produce robust and high-quality solutions suitable for real-world machine learning applications.
Risk of Premature Convergence
Premature convergence occurs when a genetic algorithm quickly settles on a suboptimal solution and stops improving.
This often happens when:
Selection is too aggressive
Diversity in the population is lost
Mutation rates are too low
Premature convergence limits exploration and prevents the discovery of better global solutions.
Strategies to Maintain Diversity
Maintaining diversity is essential for long-term optimization success. Common strategies include:
- Increasing mutation rates during stagnation
- Using diverse selection techniques
Applying controlled elitism
Introducing random individuals periodically
Adaptive operator tuning based on performance
These strategies help genetic algorithms remain flexible, avoid stagnation, and continuously improve over generations.
Advantages of Using Genetic Operators
Genetic operators provide several powerful advantages that make genetic algorithms a popular choice for optimization in machine learning. Their evolutionary nature allows them to handle complex problems that are difficult or impossible for traditional optimization techniques.
Solves Complex Optimization Problems
Genetic operators enable the exploration of large, nonlinear, and multi-dimensional search spaces. Because they do not rely on gradients or mathematical assumptions, genetic algorithms can solve highly complex optimization problems where traditional methods struggle.
Works with Noisy or Incomplete Data
Machine learning systems often deal with real-world data that is noisy, uncertain, or partially missing. Genetic operators are robust to such imperfections because they evaluate populations of solutions rather than relying on precise calculations. This population-based approach allows the algorithm to adapt even when data quality is imperfect.
Avoids Local Optima
One of the strongest advantages of genetic operators is their ability to escape local optima. By maintaining population diversity and introducing randomness through mutation, genetic algorithms continue exploring the solution space and increase the likelihood of finding global optimal solutions.
Flexible and Model-Agnostic
Genetic operators can be applied to a wide range of machine learning models without requiring model-specific modifications. Whether the task involves decision trees, neural networks, clustering, or rule-based systems, genetic operators can optimize parameters, structures, or feature subsets effectively.
Easy to Hybridize with Other ML Techniques
Genetic operators integrate easily with other optimization and learning methods. They are commonly combined with:
- Gradient-based optimization
- Reinforcement learning
- Deep learning architectures
These hybrid approaches leverage the strengths of genetic operators for global search and other techniques for fine-tuning, resulting in more efficient and powerful machine learning systems.
Challenges and Limitations
While genetic operators offer powerful optimization capabilities, they also come with certain challenges and limitations. Understanding these drawbacks helps practitioners decide when genetic algorithms are appropriate and how to use them effectively.
Computational Cost
- Genetic algorithms often require evaluating many candidate solutions across multiple generations. This population-based approach can be computationally expensive, especially when fitness evaluations involve complex machine learning models or large datasets. As a result, genetic operators may demand significant processing power and time.
Slow Convergence for Large Datasets
- For high-dimensional problems or very large datasets, genetic algorithms may converge more slowly than gradient-based methods. While they excel at global exploration, fine-tuning solutions can take many generations, making them less efficient for problems where faster convergence is critical.
Parameter Tuning Complexity
- The performance of genetic operators depends heavily on parameters such as population size, mutation rate, crossover rate, and selection pressure. Poorly chosen parameters can lead to premature convergence, excessive randomness, or inefficient learning. Finding the right balance often requires experimentation and experience.
Requires Domain Understanding
- Although genetic algorithms are flexible, designing effective fitness functions and selecting appropriate operators often requires domain knowledge. Without a clear understanding of the problem space, the algorithm may evolve solutions that are technically optimal but practically ineffective.
Not Always the Best Optimizer
- Genetic operators are not a universal solution. For problems with smooth, well-defined gradients, traditional optimization methods like gradient descent may be faster and more efficient. Genetic algorithms are best suited for complex, non-linear, or poorly understood optimization problems rather than simple or well-structured tasks.
Future Trends and Applications
As machine learning systems become more complex and data-driven, genetic operators are evolving to meet modern optimization demands. Advances in computing power and algorithm design are expanding their role across next-generation AI systems.
Integration with Deep Learning
Neuroevolution
Neuroevolution refers to the use of genetic algorithms to optimize neural networks, including their weights, architectures, and learning rules. Instead of relying solely on backpropagation, genetic operators evolve neural structures over generations.
This approach is especially valuable for:
- Non-differentiable neural components
- Sparse or unconventional architectures
- Environments where gradient information is unreliable
Neuroevolution is gaining attention for automating neural architecture design and improving learning robustness.
Use in Reinforcement Learning
Policy Optimization
In reinforcement learning, genetic operators are increasingly used to optimize policies directly. Instead of learning through reward gradients alone, policies evolve based on performance across episodes.
This evolutionary approach:
- Works well in noisy or delayed reward environments
- Avoids unstable gradient updates
- Enables parallel policy exploration
Genetic algorithms are particularly effective for complex control and simulation-based learning tasks.
Use in Reinforcement Learning
Policy Optimization
In reinforcement learning, genetic operators are increasingly used to optimize policies directly. Instead of learning through reward gradients alone, policies evolve based on performance across episodes.
This evolutionary approach:
- Works well in noisy or delayed reward environments
- Avoids unstable gradient updates
- Enables parallel policy exploration
Genetic algorithms are particularly effective for complex control and simulation-based learning tasks.
Hybrid Optimization Algorithms
GA + Gradient-Based Methods
Hybrid optimization combines the global search ability of genetic algorithms with the fast convergence of gradient-based techniques. In such systems:
- Genetic operators explore the search space broadly
- Gradient-based methods fine-tune promising solutions
This synergy results in faster convergence, better solution quality, and improved scalability for large machine learning models.
Ongoing Research Areas (2026+)
Adaptive Genetic Operators
Future genetic algorithms dynamically adjust operator probabilities based on learning progress. Adaptive mutation and crossover rates help maintain diversity while accelerating convergence, making optimization more efficient and self-regulating.
Auto-ML Systems
Genetic operators are becoming a core component of automated machine learning systems. They enable automatic feature selection, model architecture design, and hyperparameter tuning without human intervention.
Large-Scale Parallel Evolutionary Learning
With advances in distributed and cloud computing, large populations can evolve in parallel across multiple machines. This scalability allows genetic algorithms to tackle high-dimensional, real-world problems more efficiently than ever before.
Frequently Asked Questions (FAQs)
1. What do genetic operators mean in machine learning?
Genetic operators are mechanisms used in evolutionary algorithms to modify and improve candidate solutions by simulating processes such as reproduction, variation, and survival.
Why are genetic operators essential for machine learning optimization?
They enable efficient exploration of complex solution spaces, helping machine learning models find better solutions where traditional optimization methods may fail.
Which genetic operators are commonly used?
The most widely used genetic operators include selection, crossover, mutation, and elitism, each serving a unique role in the evolutionary process.
How does the selection operator improve solutions?
Selection identifies high-performing solutions based on fitness and prioritizes them for reproduction, increasing the likelihood of better outcomes in future generations.
What role does crossover play in genetic algorithms?
Crossover merges information from two parent solutions to generate new offspring, allowing beneficial characteristics to be combined and refined.
Why is mutation necessary in evolutionary algorithms?
Mutation introduces random changes that maintain population diversity and help the algorithm explore new regions of the solution space.
What is elitism, and why is it used?
Elitism ensures that the best-performing solutions are retained unchanged in the next generation, protecting high-quality results from being lost.
How do genetic operators enhance machine learning models?
They assist in optimizing parameters, selecting relevant features, and evolving model structures to improve accuracy and robustness.
Can genetic operators be applied without gradient information?
Yes. Genetic operators work independently of gradients, making them suitable for problems with non-differentiable or noisy objective functions.
What types of machine learning problems use genetic operators?
They are commonly applied to feature selection, hyperparameter tuning, clustering, rule learning, and neural network optimization.
What makes genetic operators different from traditional optimization methods?
Unlike gradient-based methods, genetic operators use population-based search and randomness, enabling better global exploration.
What are the key benefits of using genetic operators?
They handle complex optimization tasks, adapt to uncertain data, and reduce the risk of getting trapped in suboptimal solutions.
What challenges come with genetic operators?
Genetic algorithms can be computationally intensive, require parameter tuning, and may converge slowly for large-scale problems.
Are genetic operators used in real-world systems?
Yes. They are widely used in finance, logistics, healthcare, bioinformatics, and automated machine learning platforms.
Do genetic operators have a future in AI development?
Absolutely. They continue to evolve and are increasingly integrated with deep learning, reinforcement learning, and AutoML frameworks.





